Schläfli symbol

The dodecahedron is a regular polyhedron with Schläfli symbol {5,3}, having 3 pentagons around each vertex.

In geometry, the Schläfli symbol is a notation of the form {p,q,r,...} that defines regular polytopes and tessellations.

The Schläfli symbol is named after the 19th-century mathematician Ludwig Schläfli who made important contributions in geometry and other areas.

1 Description
2 Symmetry groups
3 Regular polygons (plane)
4 Regular polyhedra (3-space)
5 Regular polychora (4-space)
6 Higher dimensions
7 Dual polytopes
8 Uniform prismatic polytopes
9 Extension to Schläfli symbols
10 References
11 External links

Description

The Schläfli symbol is a recursive description, starting with a p-sided regular polygon as {p}. For example, {3} is an equilateral triangle, {4} is a square and so on.

A regular polyhedron which has q regular p-gon faces around each vertex is represented by {p,q}. For example, the cube has 3 squares around each vertex and is represented by {4,3}.

A regular 4-polytope with r {p,q} regular polyhedral cells around each edge is represented by {p,q,r}, and so on.

Regular polytopes can have star polygon elements, like the pentagram, with symbol {5/2}, represented by the vertices of a pentagon but connected alternately.

A facet of a regular polytope {p,q,r,...,y,z} is {p,q,r,...,y}. There are z facets around each vertex.

A regular polytope has a regular vertex figure. The vertex figure of a regular polytope {p,q,r,...} is {q,r,...}.

The Schläfli symbol can represent a finite convex polyhedron, an infinite tessellation of Euclidean space, or an infinite tessellation of hyperbolic space, depending on the angle defect of the construction. A positive angle defect allows the vertex figure to fold into a higher dimension and loops back into itself as a polytope. A zero angle defect will tessellate space of the same dimension as the facets. A negative angle defect can't exist in ordinary space, but can be constructed in hyperbolic space.

Usually a vertex figure is assumed to be a finite polytope, but can sometimes be considered a tessellation itself.

A regular polytope also has a dual polytope, represented by the Schläfli symbol elements in reverse order. A self-dual regular polytope will have a symmetric Schläfli symbol.

Symmetry groups

A Schläfli symbol is closely related to reflection symmetry groups, also called Coxeter groups, given with the same indices, but square brackets instead [p,q,r,...]. Such groups are often named by the regular polytopes they generate. For example [3,3] is the Coxeter group for Tetrahedral symmetry, and [3,4] is octahedral symmetry, and [3,5] is icosahedral symmetry.

Regular polygons (plane)

The Schläfli symbol of a regular polygon with n edges is {n}.

For example, a regular pentagon is represented by {5}.

See the convex regular polygon and nonconvex star polygon.

For example, {5/2} is the pentagram.

Regular polyhedra (3-space)

The Schläfli symbol of a regular polyhedron is {p,q} if its faces are p-gons, and each vertex is surrounded by q faces (the vertex figure is a q-gon).

For example {5,3} is the regular dodecahedron. It has pentagonal faces, and 3 pentagons around each vertex.

See the 5 convex Platonic solids, the 4 nonconvex Kepler-Poinsot polyhedra.

Schläfli symbols may also be defined for regular tessellations of Euclidean or hyperbolic space in a similar way.

For example, the hexagonal tiling is represented by {6,3}.

Regular polychora (4-space)

The Schläfli symbol of a regular polychoron is of the form {p,q,r}. Its (two-dimensional) faces are regular p-gons ({p}), the cells are regular polyhedra of type {p,q}, the vertex figures are regular polyhedra of type {q,r}, and the edge figures are regular r-gons (type {r}).

See the six convex regular and 10 nonconvex polychora.

For example, the 120-cell is represented by {5,3,3}. It is made of dodecahedron cells {5,3}, and has 3 cells around each edge.

There is also one regular tessellation of Euclidean 3-space: the cubic honeycomb, with a Schläfli symbol of {4,3,4}, made of cubic cells, and 4 cubes around each edge.

There are also 4 regular hyperbolic tessellations including {5,3,4}, the Hyperbolic small dodecahedral honeycomb, which fills space with dodecahedron cells.

Higher dimensions

For higher dimensional polytopes, the Schläfli symbol is defined recursively as {p₁, p₂, ..., p_n − 1} if the facets have Schläfli symbol {p₁,p₂, ..., p_n − 2} and the vertex figures have Schläfli symbol {p₂,p₃, ..., p_n − 1}.

Notice that a vertex figure of a facet of a polytope and a facet of a vertex figure of the same polytope are the same: {p₂,p₃, ..., p_n − 2}.

There are only 3 regular polytopes in 5 dimensions and above: the simplex, {3,3,3,...,3}; the cross-polytope, {3,3, ... ,3,4}; and the hypercube, {4,3,3,...,3}. There are no non-convex regular polytopes above 4 dimensions.

Dual polytopes

If a polytope of dimension ≥ 2 has Schläfli symbol {p₁,p₂, ..., p_n − 1} then its dual has Schläfli symbol {p_n − 1, ..., p₂,p₁}.

If the sequence is palindromic, i.e. the same forwards and backwards, the polytope is self-dual. Every regular polytope in 2 dimensions (polygon) is self-dual.

Uniform prismatic polytopes

Prismatic uniform polytopes can be defined and named as a Cartesian product of lower dimensional regular polytopes:

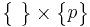A p-gonal prism, with vertex figure p. 4.4 as $\begin{Bmatrix}\ \end{Bmatrix} \times \begin{Bmatrix} p \end{Bmatrix}$ .
A uniform {p,q}-hedral prism as $\begin{Bmatrix}\ \end{Bmatrix} \times \begin{Bmatrix} p,q \end{Bmatrix}$ .
A uniform p-q duoprism as $\begin{Bmatrix} p \end{Bmatrix} \times \begin{Bmatrix} q \end{Bmatrix}$ .

Extension to Schläfli symbols

Coxeter expanded his usage of the Schläfli symbol to quasiregular polyhedron by adding a vertical dimension to the symbol. It was a starting point towards the more general Coxeter-Dynkin diagram.

Form	Extended Schläfli symbol	t-notation
Regular	$\begin{Bmatrix} p , q \end{Bmatrix}$	t₀{p,q}
Quasiregular	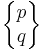$\begin{Bmatrix} p \\ q \end{Bmatrix}$	t₁{p,q}
Regular dual	$\begin{Bmatrix} q , p \end{Bmatrix}$	t₂{p,q}

And for rectified 4-polytopes:

Form	Extended Schläfli symbol	t-notation
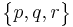Regular	$\begin{Bmatrix} p, q , r \end{Bmatrix}$	t₀{p,q,r}
Rectified	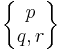$\begin{Bmatrix} p \\ q , r \end{Bmatrix}$	t₁{p,q,r}
Rectified dual	$\begin{Bmatrix} q , p \\ r \end{Bmatrix}$	t₂{p,q,r}
Regular dual	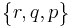$\begin{Bmatrix} r, q , p \end{Bmatrix}$	t₃{p,q,r}